আপেক্ষিকতা
আপেক্ষিকতা: নিউটনীয় পদার্থ বিদ্যা অনুসারে গতিশীল ঘড়ি ও নিশ্চল ঘড়ি একই সময় দেবে, পর্যবেক্ষকের গতি যাই হোক না কেনো, সকল বস্তুর দৈর্ঘ্য সমান হবে, আবার বস্তু যে গতিতেই চলুক না কেন, তার ভর সমান হবে। কিন্তু আইনস্টাইনের আপেক্ষিক তত্ত্বের মতে গতিশীল ঘড়ি ধীরে চলে, গতিশীল বস্তুর দৈর্ঘ কমে যায় ও ভর বৃদ্ধি পায়। তবে শর্ত থাকে যে বস্তুর গতি অবশ্যই আলোর গতির কাছা কাছি হতে হবে, বা আলোর গতির সাথে তুলোননীয় হতে হবে। আরও উল্লেখ্য থাকে যে কোন বস্তুর পক্ষে কোন ভাবেই আলোর সমান গতিবেগ অর্জন করা সম্ভব নয়।
কাল দীর্ঘায়ন(Time Dilation): কোন পর্যবেক্ষকের সাপেক্ষে গতিশীল অবস্থায় সংঘটিত দুটি ঘটনার মধ্যবর্তী কাল ব্যবধান ঐ পর্যবেক্ষকের সাপেক্ষে নিশ্চল অবস্থায় সংঘটিত ঐ একই ঘটনাদ্বয়ের মধ্যবর্তী কাল ব্যবধানের চেয়ে বেশি। এই প্রভাবকে কাল দীর্ঘায়ন বলে।
ধরা যাক, মহাশূন্যযানে অবস্থানকারী কোন ব্যক্তি দুটি ঘটনার মধ্যবর্তী সময় বা কাল ব্যবধান t নির্নয় করলেন। ভূপৃষ্ট থেকে কোন ব্যক্তি ঐ সময় ব্যবধান t0 নির্ণয় করলেন। মহাশূন্যযানের গতিবেগ v ও আলোর বেগকে c দিয়ে প্রকাশ করলে।
\( t_0 = \frac{t}{\sqrt{1-\frac{v^2}{c^2}}} \)
এখানে \(\sqrt{1-\frac{v^2}{c^2}}\) রাশিটি সব সময় 1 এর চেয়ে ছোট তাই t0 সবসময়ই t থেকে বড়।
তাই নিশ্চল কাঠামোতে অবস্থিত একটি ঘড়ি গতিশীল কাঠামোতে সংঘটিত ঘটনাগুলোর মধ্যবর্তী কাল ব্যবধান গতিশীল কাঠামোতে অবস্থিত ঘড়ির চেয়ে অধিক নির্ণয় করবে।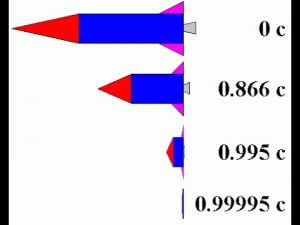
দৈর্ঘ্য সংকোচন(Length Contraction): কোন পর্যবেক্ষকের সাপেক্ষে গতিশীল বস্তুর দৈর্ঘ্য ঐ পর্যবেক্ষকের সাপেক্ষে নিশ্চল অবস্থায় ঐ একই বস্তুর দৈর্ঘের চেয়ে ছোট হয়, এপ্রভাবকে দৈর্ঘ্য সংকোচন বলে।
L -পর্যবেক্ষকের সাপেক্ষে গতিশীল অবস্থার দৈর্ঘ।
L0 – পর্যবেক্ষকের সাপেক্ষে নিশ্চল অবস্থার দৈর্ঘ্য হলে
দৈর্ঘ্য সংকোচনের সমীকরণটি হল
\( L_0 = \frac{L}{\sqrt{1-\frac{v^2}{c^2}}} \)
যেহেতু \( \sqrt{1-\frac{v^2}{c^2}} \)সবসময়ই 1 এর চেয়ে ছোট তাই, L সবসময়ই L0 অপেক্ষা ছোট। অর্থাৎ নিশ্চল অবস্থার L0 বড় হবে। সুতরাং কোন দণ্ডের গতিশীল অবস্থার দৈর্ঘ্য দণ্ডটির নিশ্চল অবস্থার দৈর্ঘ্যের চেয়ে ছোট হবে।
ভরের আপেক্ষিকতা(Relativity of Mass): কোন বস্তুর নিশ্চল অবস্থার ভর m0 ও গতিশীল অবস্থার ভর যদি m হয়। তবে m0 ও m এর মধ্যে সম্পর্ক হবে
\( m = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\) \(\Rightarrow\) \({ m_0 = m \sqrt{1-\frac{v^2}{c^c}}} \)
অর্থাৎ গতিশীল অবস্থায় ভর বৃদ্ধি পাচ্ছে।


